Las matemáticas se volvieron a poner de moda con el problema del cumpleaños de Cheryl en esta ocasiòn un nuevo problema se viraliza tras 20 años. ¿La razón? sólo el 10% de los estudiantes de 16 países de todo el mundo (el 4% en Estados Unidos y el 24% en Suecia) pueden resolverlo.
La asociación explicó que este problema fue el que más gente falló, a pesar de que no hace falta saber muchas matemáticas, al igual que ocurría con el problema de lógica del cumpleaños de Cheryl, que se hizo viral la semana pasada.
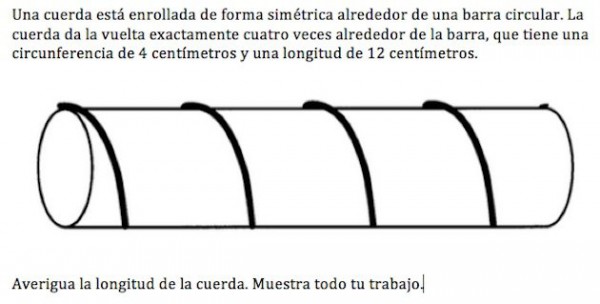
Verne cuenta lo siguiente: El problema ha empezado a correr por las redes y su enunciado es en apariencia sencillo: “Una cuerda está enrollada de forma simétrica alrededor de una barra circular. La cuerda da la vuelta exactamente cuatro veces alrededor de la barra, que tiene una circunferencia de 4 centímetros y una longitud de 12 centímetros. Averigua cuánto mide la cuerda”.
De un test internacional para estudiantes de bachillerato en 1995. ¿Cuánto mide el hilo? pic.twitter.com/OKsAyUCX60
— Principia Marsupia (@pmarsupia) abril 20, 2015
Solución
El problema no requiere saber más matemáticas que el teorema de Pitágoras. Que no cunda el pánico, lo aprendimos de niños: en todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Como se puede ver en la ilustración de la IEA, la forma más fácil de resolverlo es pensar en la barra como en una superficie plana. De este modo, vemos que en los extremos se forma un triángulo rectángulo. Sabemos que uno de los catetos mide cuatro centímetros y el otro, tres (una cuarta parte de la longitud de la barra), lo cual nos permite averiguar cuánto mide la hipotenusa. Este resultado nos basta para saber la longitud de la cuerda, ya que hay cuatro trozos iguales alrededor de la barra.
La hipotenusa es igual a la raíz cuadrada de 42 + 32. Es decir, a la raíz cuadrada de 25 (16+9), que es cinco. Como hay cuatro trozos iguales a lo largo del cilindro, la cuerda mide 20 centímetros (5*4).
Desde la IEA se explicaba que los alumnos tuvieron problemas para encontrar la equivalencia entre esta cuerda enrollada y un triángulo porque “aprender a pensar de esta forma creativa y aplicada no forma parte de ningún currículum”.
Te puede Interesar :
Ciberpiratas robaron US$45 mlls en todo el mundo en unas cuantas horas
VIDEO: Cristiano Ronaldo y el gran problema que su celebración causó
Las bebidas azucaradas matan a miles en todo el mundo, según estudio
Disminuye número de empleados a tiempo completo en todo el mundo
¿Cuáles son los países más endeudados del planeta?
Laura Bozzo se convierte en un problema para Televisa
“Mi problema con las mujeres”: Serie peruana fue vendida a la cadena ABC en EE.UU.
Última fecha de liguillas de la Copa Movistar es un problema para la ADFP
